Published on ICLR 2021
这篇文章提出了Prototypical Contrastive Learning (PCL),这是一种无监督的表示学习算法,将对比学习和聚类联系在一起。
作者认为instance-wise contrastive learning存在两个问题:
- 实例之间的判别只利用到了低价的图像之间的差异,而没有考虑到高阶的语义关系
- 只要求正负样本远离,没有考虑到负样本内部的相似性。不可避免地会有负样本对具有相似的语义,本应在表征空间中相距更近,但被对比损失拉远了。这是一种class collision问题。
Formulation
最终的目标是找到能使观察到的$n$个样本的对数似然最大化的参数$\theta$:
\[\theta^*=\underset{\theta}{\arg \max } \sum_{i=1}^n \log p\left(x_i ; \theta\right)\]假设观测到的数据集是 $\left\lbrace x_i\right\rbrace_{i=1}^n$, 对应的原型(prototype)是隐变量 $C=\left\lbrace c_i\right\rbrace_{i=1}^k$ ,则代入$C$上式化为:
\[\theta^*=\underset{\theta}{\arg \max } \sum_{i=1}^n \log p\left(x_i ; \theta\right)=\underset{\theta}{\arg \max } \sum_{i=1}^n \log \sum_{c_i \in C} p\left(x_i, c_i ; \theta\right)\]现在还是很难优化,利用Jensen’s inequality,最大化上式可以转化为最大化上式的下界:
\[\begin{align} \sum_{c_i \in C} Q\left(c_i\right)&=1 \\ \sum_{i=1}^n \log \sum_{c_i \in C} p\left(x_i, c_i ; \theta\right) &=\sum_{i=1}^n \log \sum_{c_i \in C} Q\left(c_i\right) \frac{p\left(x_i, c_i ; \theta\right)}{Q\left(c_i\right)}\\ & \geq \sum_{i=1}^n \sum_{c_i \in C} Q\left(c_i\right) \log \frac{p\left(x_i, c_i ; \theta\right)}{Q\left(c_i\right)}\\ &=\sum_{i=1}^n \sum_{c_i \in C} Q\left(c_i\right) \log p\left(x_i, c_i ; \theta\right)-\underbrace{\sum_{i=1}^n \sum_{c_i \in C} Q\left(c_i\right) \log Q\left(c_i\right)}_{\text{constant}} \end{align}\]由于第二项为常数,所以只要最大化第一项就行了:
\[\theta^*=\underset{\theta}{\arg \max }\sum_{i=1}^n \sum_{c_i \in C} Q\left(c_i\right) \log p\left(x_i, c_i ; \theta\right)\]当$\frac{p\left(x_i, c_i ; \theta\right)}{Q\left(c_i\right)}$为常数时等号成立,有:
\[Q\left(c_i\right)=\frac{p\left(x_i, c_i ; \theta\right)}{Const}\\ \sum_{c_i \in C}Q\left(c_i\right)=1=\frac{1}{Const}\sum_{c_i \in C}p\left(x_i, c_i ; \theta\right)\\ Const=\sum_{c_i \in C}p\left(x_i, c_i ; \theta\right)\]所以此时代入$Const$可以发现$Q(c_i)$就是在$x_i$条件下的后验概率$p(c_i;x_i,\theta)$:
\[Q\left(c_i\right)=\frac{p\left(x_i, c_i ; \theta\right)}{\sum_{c_i \in C} p\left(x_i, c_i ; \theta\right)}=\frac{p\left(x_i, c_i ; \theta\right)}{p\left(x_i ; \theta\right)}=p\left(c_i ; x_i, \theta\right)\]然后使用EM算法求解。
在E-step,估计$Q(c_i)$也即$p\left(c_i ; x_i, \theta\right)$。对特征$v_i^{\prime}=f_{\theta^{\prime}}\left(x_i\right)$ 使用 $k$-means 聚类形成$k$个簇,这里的$f_{\theta’}$是动量编码器。原型$c_i$定义为第$i$个簇的簇心。$Q(c_i)$定义如下:
\[Q(c_i)=p\left(c_i ; x_i, \theta\right)=\mathbb{1}\left(x_i \in c_i\right)=\left\lbrace \begin{aligned} 1, x_i\in c_i\\ 0, x_i \notin c_i \end{aligned} \right.\]在M-step进行最大化:
\[\begin{aligned} \underset{\theta}{\arg \max }\sum_{i=1}^n \sum_{c_i \in C} Q\left(c_i\right) \log p\left(x_i, c_i ; \theta\right) &=\sum_{i=1}^n \sum_{c_i \in C} p\left(c_i ; x_i, \theta\right) \log p\left(x_i, c_i ; \theta\right) \\ &=\sum_{i=1}^n \sum_{c_i \in C} \mathbb{1}\left(x_i \in c_i\right) \log p\left(x_i, c_i ; \theta\right)\\ &=\sum_{i=1}^n \sum_{c_i \in C} \mathbb{1}\left(x_i \in c_i\right) \log p\left(x_i ; c_i, \theta\right) \underbrace{p\left(c_i ; \theta\right)}_{\text{uniform prior}} \\ &=\sum_{i=1}^n \sum_{c_i \in C} \mathbb{1}\left(x_i \in c_i\right) \log\frac{1}{k} \cdot p\left(x_i ; c_i, \theta\right) \end{aligned}\]假设原型$c_i$周围的样本点服从各向同性的高斯分布(isotropic Gaussian):
\[p\left(x_i ; c_i, \theta\right)=\exp \left(\frac{-\left(v_i-c_s\right)^2}{2 \sigma_s^2}\right) / \sum_{j=1}^k \exp \left(\frac{-\left(v_i-c_j\right)^2}{2 \sigma_j^2}\right)\]这里$v_i=f_\theta\left(x_i\right)$ ,$x_i \in c_s$。注意到这里有一个$c_s$和$c_i$之间的差异,因为计算的时候是对所有的样本点和所有原型之间进行计算,所以这里的$c_s$专指$x_i$所属于的那个原型。此外,这里的每一个簇的方差$\sigma_j$也是不同的。这里还有一点需要注意的是$v_i$和距离$v_i$比较远的原型$c_i$之间计算得到的相似性很低,在分母中只占较小的比重,所以这个式子也可以近似看作是只考虑了距离$v_i$最近的几个簇心后的概率分布。
最终化简之后的目标是要最小化下式:
\[\theta^*=\underset{\theta}{\arg \min } \sum_{i=1}^n-\log \frac{\exp \left(v_i \cdot c_s / \phi_s\right)}{\sum_{j=1}^k \exp \left(v_i \cdot c_j / \phi_j\right)}\]这里$\phi \propto \sigma^2$表示样本点在原型周围分布的聚集程度。注意到最终的优化目标和InfoNCE相似,所以说InfoNCE也可以解释成一种极大似然估计的特殊情况。
最终的损失函数定义如下:
\[\mathcal{L}_{\text {ProtoNCE }}=\sum_{i=1}^n-\left(\log \frac{\exp \left(v_i \cdot v_i^{\prime} / \tau\right)}{\sum_{j=0}^r \exp \left(v_i \cdot v_j^{\prime} / \tau\right)}+\frac{1}{M} \sum_{m=1}^M \log \frac{\exp \left(v_i \cdot c_s^m / \phi_s^m\right)}{\sum_{j=0}^r \exp \left(v_i \cdot c_j^m / \phi_j^m\right)}\right)\]损失函数的第一项作者把InfoNCE加入了进来,这里$v’_i$是和$v_i$属于相同簇的增广样本,$r$是负样本的数量。总共进行$M$次聚类,每次的类簇数都不一样$K=\left\lbrace k_m\right \rbrace _{m=1}^M$。通过这种方式可以提升原型的概率估计的鲁棒性,并能编码分层的结构。
$\phi$表示样本点的集中程度,使用同一簇的动量特征$\left\lbrace v_z^{\prime}\right\rbrace_{z=1}^Z$估计$\phi$。$\phi$越小,表明聚集程度越大。对于较小的$\phi$,应该满足:
- $v’_z$和$c$之间的平均距离小
- 簇包含的特征点多($Z$比较大)
所以,定义如下:
\[\phi=\frac{\sum_{z=1}^Z\left\|v_z^{\prime}-c\right\|_2}{Z \log (Z+\alpha)}\]$\alpha$是平滑系数,确保$\phi$不会太大。$\tau$通过在原型集合$C^m$上对$\phi$归一化并取均值得到。
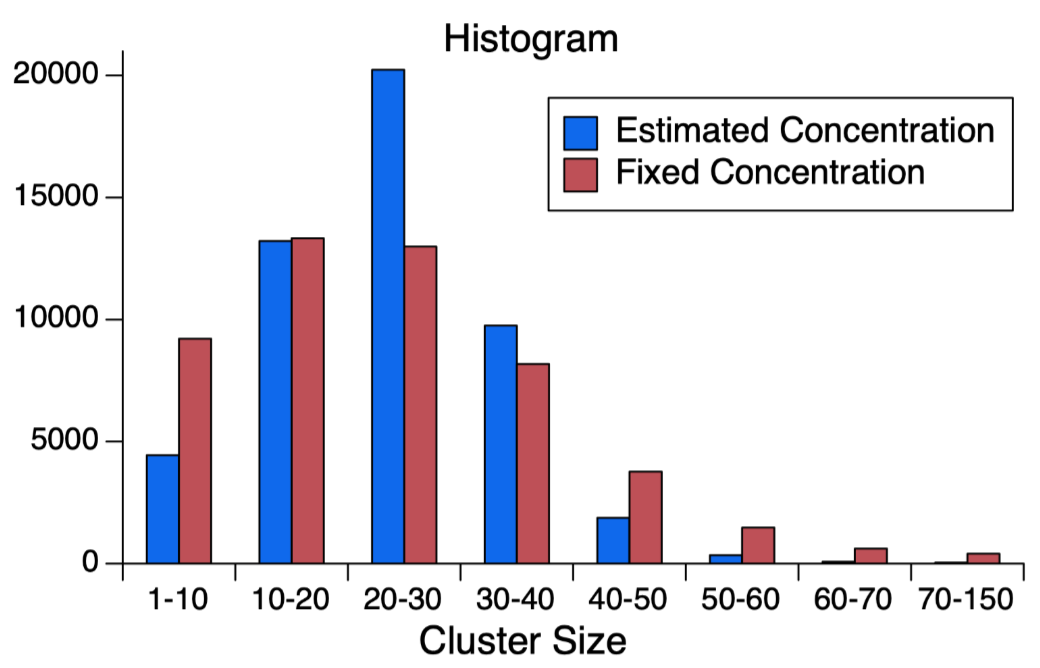
对于松散的簇($\phi$较大)来说,ProtoNCE会拉近样本embedding和原型之间距离。对于紧凑的簇($\phi$较小)来说,ProtoNCE更少地使样本的embedding接近原型。所以ProtoNCE将会产生更加平衡的簇,且簇的聚集程度都较为相似。这还阻止了所有embedding都坍塌到同一个簇的这种平凡解(DeepCluster里面通过数据重采样解决了这个问题)。如下图所示,引入对聚集程度的估计使得簇的大小分布更为集中,固定的聚集程度的簇的大小更分散。
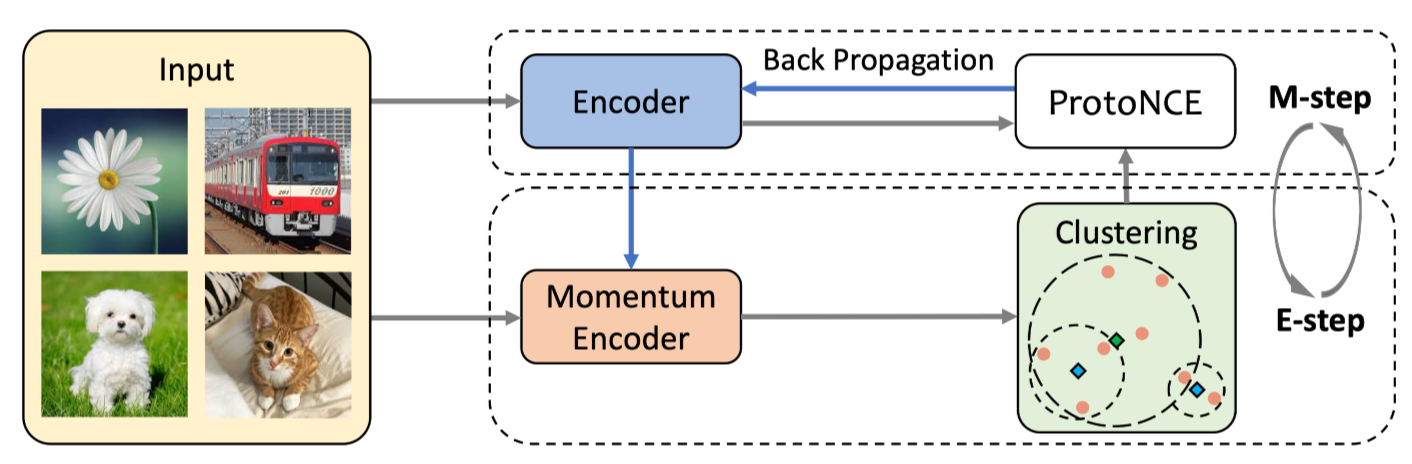
下图是模型的框架图:
互信息分析
我们已经知道最小化InfoNCE等价于最大化$V$和$V’$之间互信息。相似地,最小化本文提到的ProtoNCE等价于最大化$V$和$\lbrace V’,C^1,\dots,C^M\rbrace$之间的互信息。这带来的优势有两方面:
-
这种情况下编码器能够学习到原型之间共享信息,这就忽略了原型内部的噪声,使得这种共享的信息更可能捕获高阶的语义知识。
-
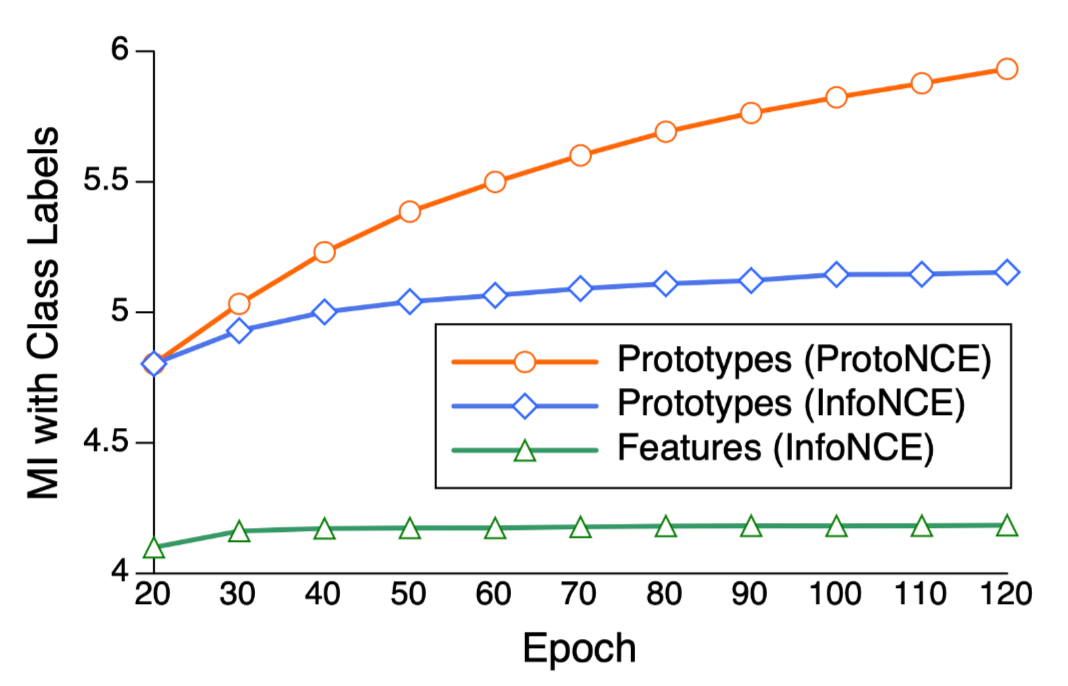
和样本特征相比,原型和类别标签之间的互信息更大。如下图所示,在训练过程中,embedding和类别标签之间的互信息是不断增加的。但是可以看到原型和类别标签之间的互信息是最大的,单纯的样本特征和类别标签的互信息是比较小的。ProtoNCE带来的互信息增益是大于InfoNCE的。这说明原型确实是学到了更丰富的语义。
实验
在训练过程中有一个需要注意的细节是作者先只用InfoNCE训练模型20轮以warm-up,然后再用本文中的loss。
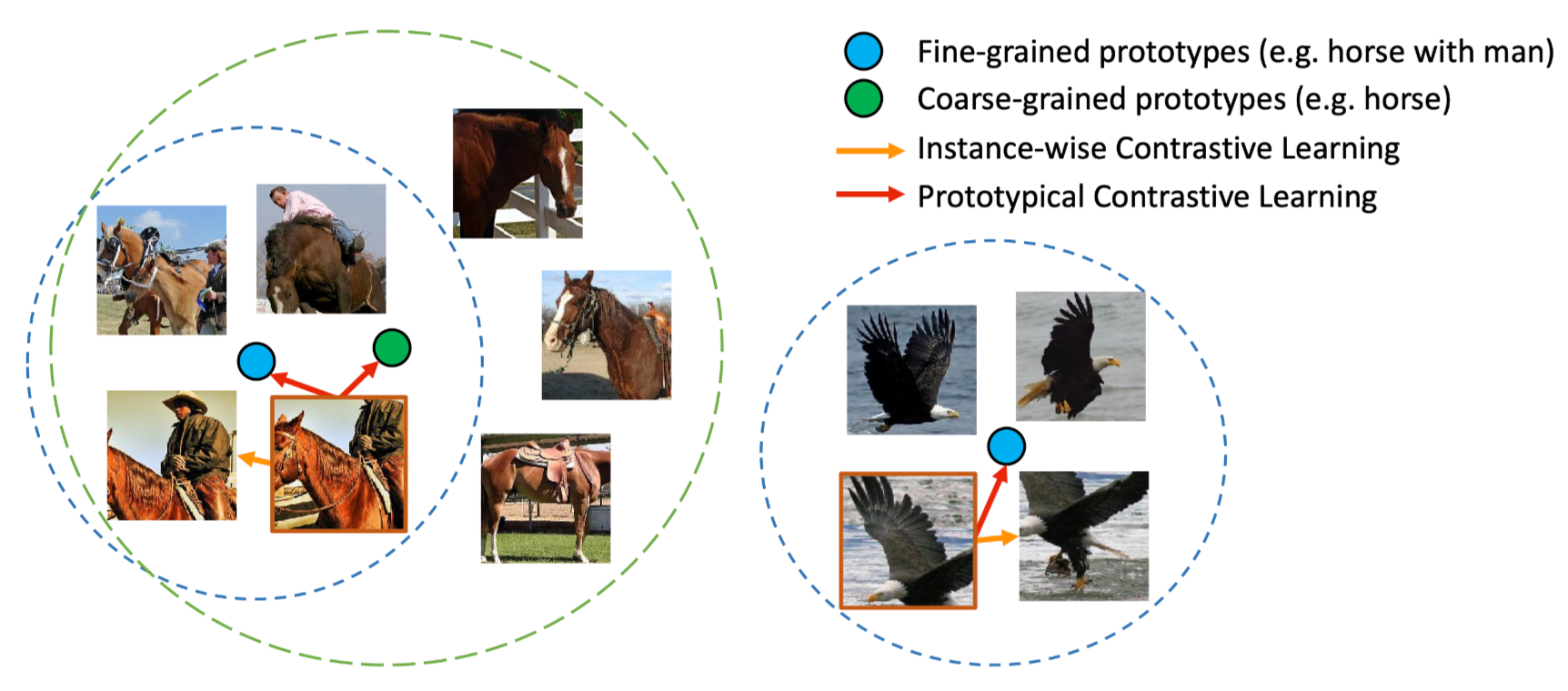
这张图片展示了该算法可以学到不同粒度的高阶语义。这里的不同粒度是由聚类时预先指定的类簇数$k$所决定的,$k$越大,粒度越细,反之粒度则粗。下图中的绿色和黄色也是表示不同的粒度,但具有相似也有差别的语义关系。


伪代码
