Published on NeurIPS 2017
这篇文章提出了原型网络(prototypical networks)用于小样本的分类问题。
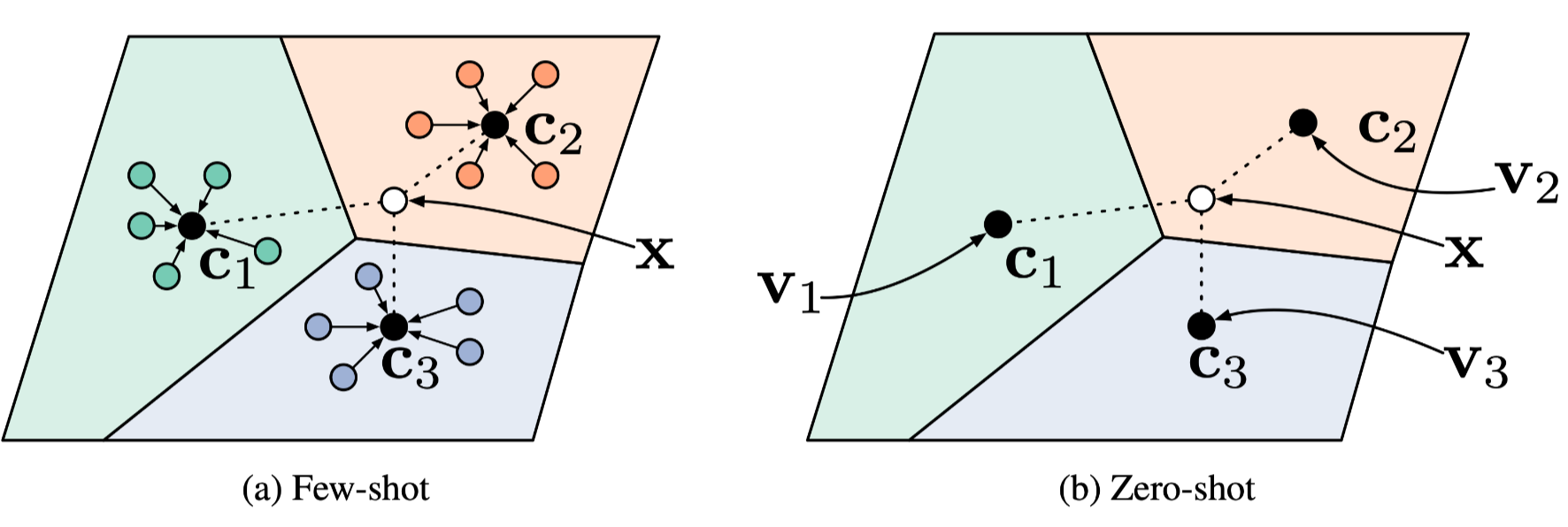
如下图所示,该模型可以应用到小样本或零样本的学习中。
Formulation
在小样本分类中,我们给定了一个小的有标签的支撑集(support set)$S=\left\lbrace \left(\mathbf{x}_1, y_1\right), \ldots,\left(\mathbf{x}_N, y_N\right)\right\rbrace $,$\mathbf{x}_i\in \mathbb{R}^D$, $y_i\in \lbrace 1,\dots,K\rbrace $是对应的标签。$S_k$表示类别$k$的有标签的样本集合。
原型网络为每一个类别通过嵌入函数 $f_\phi: \mathbb{R}^D \rightarrow \mathbb{R}^M$计算一个 $M$维的表征 $\mathbf{c}_k \in \mathbb{R}^M$, 也称为原型。这里可学习的参数是 $\phi$,计算方式如下:
\[\mathbf{c}_k=\frac{1}{\left|S_k\right|} \sum_{\left(\mathbf{x}_i, y_i\right) \in S_k} f_\phi\left(\mathbf{x}_i\right) \tag{1}\]给定一个距离函数 $d: \mathbb{R}^M \times \mathbb{R}^M \rightarrow[0,+\infty)$,基于查询点和原型之间的距离,原型网络将会输出查询点$\mathbf{x}$在所有类别上的分布:
\[p_\phi(y=k \mid \mathbf{x})=\frac{\exp \left(-d\left(f_\phi(\mathbf{x}), \mathbf{c}_k\right)\right)}{\sum_{k^{\prime}} \exp \left(-d\left(f_\phi(\mathbf{x}), \mathbf{c}_{k^{\prime}}\right)\right)}\tag{2}\]损失函数是:
\[J(\phi)=-\log p_\phi(y=k \mid \mathbf{x})\tag{3}\]$k$是$\mathbf{x}$的真实类别。
伪代码
伪代码里面的损失函数就是把上面的损失函数代入,展开之后的结果。直观理解有个距离项,让查询点$\mathbf{x}$离其所属类别的原型更近,离其他类别的原型更远。

regular Bregman divergences
这一节讨论了原型网络和regular Bregman divergences之间的关系,还有待于进一步学习。
此外,余弦距离不属于Bregman divergences,不满足这里的假设,所以在实验中也发现,欧氏距离要优于余弦距离。
欧式距离等价于线性模型
如果取$d\left(\mathbf{z}, \mathbf{z}^{\prime}\right)=\left|\mathbf{z}-\mathbf{z}^{\prime}\right|^2$,那么公式(2)等价于线性模型:
\[-\left\|f_\phi(\mathbf{x})-\mathbf{c}_k\right\|^2=-f_\phi(\mathbf{x})^{\top} f_\phi(\mathbf{x})+2 \mathbf{c}_k^{\top} f_\phi(\mathbf{x})-\mathbf{c}_k^{\top} \mathbf{c}_k\]第一项和类别$k$无关,是常数项。所以可以重写为:
\[2 \mathbf{c}_k^{\top} f_\phi(\mathbf{x})-\mathbf{c}_k^{\top} \mathbf{c}_k=\mathbf{w}_k^{\top} f_\phi(\mathbf{x})+b_k, \text { where } \mathbf{w}_k=2 \mathbf{c}_k \text { and } b_k=-\mathbf{c}_k^{\top} \mathbf{c}_k\]尽管这里是一个线性函数的形式,但是$f_\phi$可以学到非线性的表征,所以证明了欧氏距离的作用。
和匹配网络(Matching Networks)的比较
在one-shot学习中,$\mathbf{c}_k=\mathbf{x}_k$,匹配网络等价于原型网络。
一个很自然的问题是在每一类中使用多个原型,而不是一个的情况是不是有意义的。这需要一种划分策略,在下面两篇文中有提及。
- Distance-based image classification: Generalizing to new classes at near-zero cost
- Metric learning with adaptive density discrimination
零样本学习
在零样本学习中,没有支撑集,对于每一类只有一个类的元数据向量$\mathbf{v}k$。为了使用原型网络,直接定义$\mathbf{c}_k=g{\vartheta}\left(\mathbf{v}_k\right)$。