Published on ICLR 2016
首先作者认为目前的距离度量学习存在两个大问题:
- 基于类别标签的监督信息使得相同类别的样本靠近,不同类别的样本远离。这既没有考虑到类内的不相似性,也没考虑到类间的相似性。
- 现有的Triplet loss或者contrastive loss仅仅惩罚样本对或者样本的三元组,并没有考虑到contextual信息,即周围的邻居结构。这不但增加了计算的复杂度,而且增大了收敛的难度。
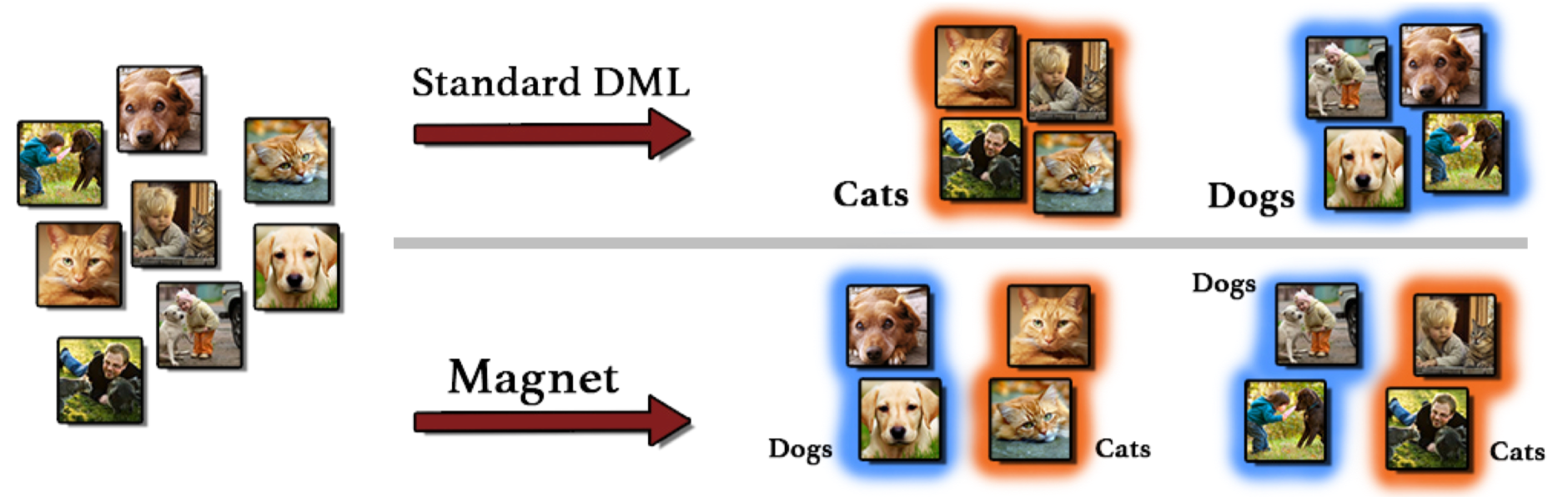
所以理想的DML算法应该是这样的:
- 追求局部的分离,而不是全局的分离。
- 分离表征空间中不同类别的分布
所以DML算法要发现不同类别之间的重叠部分,并减少惩罚这种重叠以获得判别。
所以,需要有聚类算法建模样本的分布。这样可以从直接优化样本转变成优化类簇。同时,基于聚类的算法也降低了负采样的成本,只需要两步,首先先找到相邻的簇,然后再从簇中采样即可。
Formulation
假设现在有数据集包含 $N$ 个输入和标签对 $\mathcal{D}=\left\lbrace \mathbf{x}_n, y_n\right \rbrace _{n=1}^N$ ,标签有 $C$ 类。输入样本$\mathbf{x}_n$的表征向量由映射$\mathbf{f}(\cdot ; \boldsymbol{\Theta})$计算:
\[\mathbf{r}_n=\mathbf{f}\left(\mathbf{x}_n ; \boldsymbol{\Theta}\right), n=1, \ldots, N\]对于一组类别为 $c$ 的样本, 利用K-means算法,将其分成$K$簇 $\mathcal{I}_1^c, \ldots, \mathcal{I}_K^c$,目标是要最小化每一簇内样本和其中心点$\mathbf{\mu}^c_k$的距离:
\[\begin{aligned} \mathcal{I}_1^c, \ldots, \mathcal{I}_K^c &=\arg \min _{I_1^c, \ldots, I_K^c} \sum_{k=1}^K \sum_{\mathbf{r} \in I_k^c}\left\|\mathbf{r}-\boldsymbol{\mu}_k^c\right\|_2^2 \\ \boldsymbol{\mu}_k^c &=\frac{1}{\left|I_k^c\right|} \sum_{\mathbf{r} \in I_k^c} \mathbf{r} \end{aligned}\]定义 $C(\mathbf{r})$ 为表征 $\mathbf{r}$ 的类别标签, $\boldsymbol{\mu}(\mathbf{r})$ 是其对应的簇心。 则目标函数(Magnet loss)定义如下:
\[\mathscr{L}(\boldsymbol{\Theta})=\frac{1}{N} \sum_{n=1}^N\left\{-\log \frac{e^{-\frac{1}{2 \sigma^2}\left\|\mathbf{r}_n-\boldsymbol{\mu}\left(\mathbf{r}_n\right)\right\|_2^2-\alpha}}{\sum_{c \neq C\left(\mathbf{r}_n\right)} \sum_{k=1}^K e^{-\frac{1}{2 \sigma^2}\left\|\mathbf{r}_n-\boldsymbol{\mu}_k^c\right\|_2^2}}\right\}_{+}\tag{1}\]这里$\lbrace\cdot\rbrace_+$表示hinge函数。$\alpha \in \mathbb{R}$,$\sigma^2=\frac{1}{N-1} \sum_{\mathbf{r} \in \mathcal{D}}|\mathbf{r}-\boldsymbol{\mu}(\mathbf{r})|_2^2$表示样本距离其中心的方差。
直观理解,在分子项,这个目标函数要最小化$\mathbf{r}_n$和$\boldsymbol{\mu}\left(\mathbf{r}_n\right)$之间的距离。对于分母项,该目标函数要最大化$\mathbf{r}_n$和标签与$\mathbf{r}_n$不相同的其他簇心的距离。此外对于分母项来说,和$\mathbf{r}_n$距离较远的簇之间的计算项接近0,可以忽略,所以在实际的计算过程中可以只计算局部邻居就行。这就引出了下文要提到的邻居采样过程。
效果演示
下图中的白点代表同一个类别里面的不同的簇,这里$K=32$。红箭头表示和那些指出的簇最近的样本。(a)和(b)属于不同类别,但都有动物和人的这一层含义,所虽然属于不同类别,但在空间上更靠近。(b)和(c)属于同一类别Manta,但是(b)表示的是Manta和人,(c)表示的是Manta在深水,所以在空间上距离较远。(c)和(d)属于不同类别,但表示相似的含义(in the deep),所以在空间上距离也更近。可以看到蓝色这一小簇明显是离群了,而这是Triplet和Softmax里面所没有的。

训练过程
邻居采样
在训练过程中,minbatch构建于局部邻居,而不是随机的独立采样。过程如下:

在训练时会保存每个样本的loss,对于某个簇$I$,可以计算这个簇的平均loss,$\mathscr{L}I$。定义$p{\mathcal{I}}(I) \propto \mathscr{L}_I$,即根据簇loss的大小按概率采样。即簇的loss越大,有更高的概率被采样到。基于簇loss进行采样的一个优点是可能经过几次迭代,所有的簇都能彼此分离,因为在这个过程中会优先优化那些loss很高的簇,这提高了计算效率。而如果随机采样的话,可能会导致多次对同一个簇进行优化,这就降低了计算效率。
impostor clusters直译是冒名顶替的簇,其实就是指周围的簇。$P_{I_m}(\cdot)$是均匀分布,即簇内的样本是均匀采样的。感觉这里采样簇内样本的设计还有改进的空间。
然后基于采样的样本可以计算公式(1)的近似版:
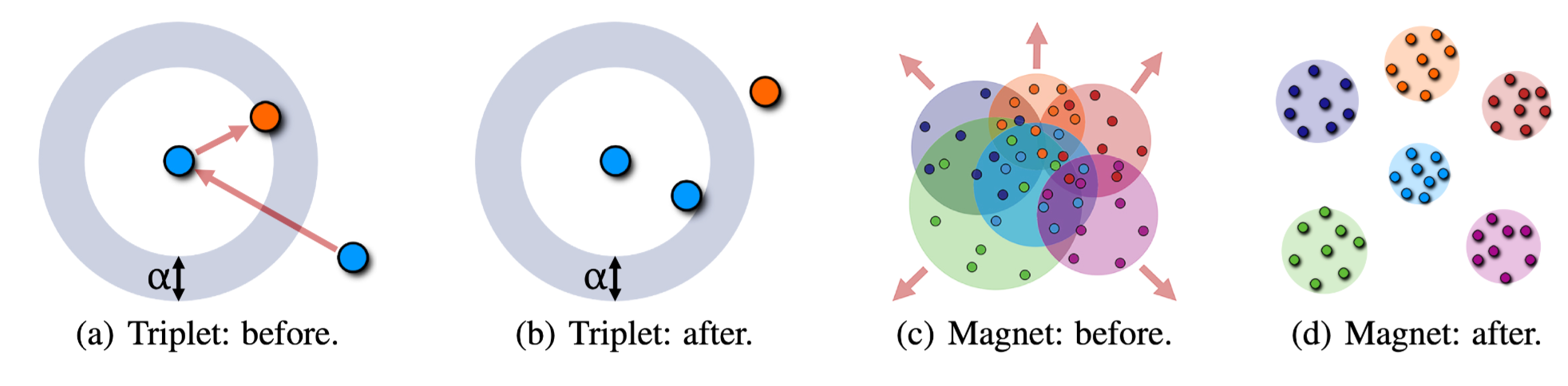
\[\hat{\mathscr{L}}(\boldsymbol{\Theta})=\frac{1}{M D} \sum_{m=1}^M \sum_{d=1}^D\left\{-\log \frac{e^{-\frac{1}{2 \hat{\sigma}^2}\left\|\mathbf{r}_d^m-\hat{\boldsymbol{\mu}}_m\right\|_2^2-\alpha}}{\sum_{\hat{\boldsymbol{\mu}}: C(\hat{\boldsymbol{\mu}}) \neq C\left(\mathbf{r}_d^m\right)} e^{-\frac{1}{2 \hat{\sigma}^2}\left\|\mathbf{r}_d^m-\hat{\boldsymbol{\mu}}\right\|_2^2}}\right\}+\tag{2}\\ \hat{\boldsymbol{\mu}}_m=\frac{1}{D} \sum_{d=1}^D \mathbf{r}_d^m\\ \hat{\sigma}=\frac{1}{M D-1} \sum_{m=1}^M \sum_{d=1}^D\left\|\mathbf{r}_d^m-\hat{\boldsymbol{\mu}}_m\right\|_2^2\]下图展示了Triplet loss和本文提出的Magnet loss之间的对比。这里有两点对比:
- Triplet loss每次只计算一个样本的三元组,而Magnet loss每次计算的是一组局部邻居样本形成的簇。三元组的设计提高了计算的复杂度和计算量。
- Triplet loss定义的是相似度是基于样本的,Magnet loss定义的相似度是基于簇分布的。Triplet loss惩罚的是样本之间的相似性,而Magnet loss惩罚的是簇之间的重叠度,并没有明确要求样本对之间的距离,所以为建模同类样本内部之间的差异性和不同类样本之间相似性打下了基础。而且,对簇的惩罚使得对样本点的调整更加具有一致性,而Triplet loss里面的三元组并不具有样本间的一致性。
评估过程
由于数据本身带有标签,每个簇也都有标签,所以可以根据最后的表征向量和邻近的簇之间的距离判断这个样本的标签,用来评估模型的效果。换句话说,样本$\mathbf{x}_n$的标签是其与最近的$L$个簇($\mathbf{\mu}_1, \ldots, \mathbf{\mu}_L$)的softmax相似度:
\[c_n^*=\arg \max _{c=1, \ldots, C} \frac{\sum_{\boldsymbol{\mu}_l: C\left(\boldsymbol{\mu}_l\right)=c} e^{-\frac{1}{2 \sigma^2}\left\|\mathbf{r}_n-\boldsymbol{\mu}_l\right\|_2^2}}{\sum_{l=1}^L e^{-\frac{1}{2 \sigma^2}\left\|\mathbf{r}_n-\boldsymbol{\mu}_l\right\|_2^2}}\]分子是计算样本和类别标签为$c$的所有临近的簇$\mu_l$之间的距离之和。这和$k$-近邻的想法一样。
和现有模型的联系
当$M=2$,$D=2$时,公式(2)退化成Triplet loss。
Neighbourhood Components Analysis
NCA的目标函数如下:
\[\mathscr{L}_{\mathrm{NCA}}(\boldsymbol{\Theta})=\frac{1}{N} \sum_{n=1}^N-\log \frac{\sum_{n^{\prime}: C\left(\mathbf{r}_{n^{\prime}}\right)=C\left(\mathbf{r}_n\right)} e^{-\left\|\mathbf{r}_n-\mathbf{r}_n^{\prime}\right\|_2^2}}{\sum_{n^{\prime}=1}^N e^{-\left\|\mathbf{r}_n-\mathbf{r}_n^{\prime}\right\|_2^2}}\]可以看到,该目标函数的目的是最小化同一类样本内部的样本点之间的距离。作者指出了该模型的一个问题是缺少一个像本文中的邻居采样过程,计算复杂度较高。
Nearest Class Mean
这里的均值向量$\boldsymbol{\mu}_c$是固定住的,可以看到$\boldsymbol{\mu}_c$是根据样本的raw embedding计算的。目的是学习变换$\boldsymbol{W}$。
\[\mathscr{L}_{\mathrm{NCM}}(\mathbf{W})=\frac{1}{N} \sum_{n=1}^N-\log \frac{e^{-\left\|\mathbf{W} \mathbf{x}_n-\mathbf{W} \boldsymbol{\mu}_{c\left(\mathbf{x}_n\right)}\right\|_2^2}}{\sum_{c=1}^C e^{-\left\|\mathbf{W} \mathbf{x}_n-\mathbf{W} \boldsymbol{\mu}_c\right\|_2^2}}\\ \boldsymbol{\mu}_c=\frac{1}{|C|} \sum_{c(\mathbf{x})=c} \mathbf{x},\; c=1, \ldots, C\]实验
在实验细节里面,作者提到在开始训练DML算法之前,先用一个部分训练的softmax warm-start DML模型的权重是一件有用的事情。但是不要用完全训练好的模型权重。所以在本文中,先用一个在ImageNet上训练了3轮的网络来初始化编码器的权重。
Attribute distribution
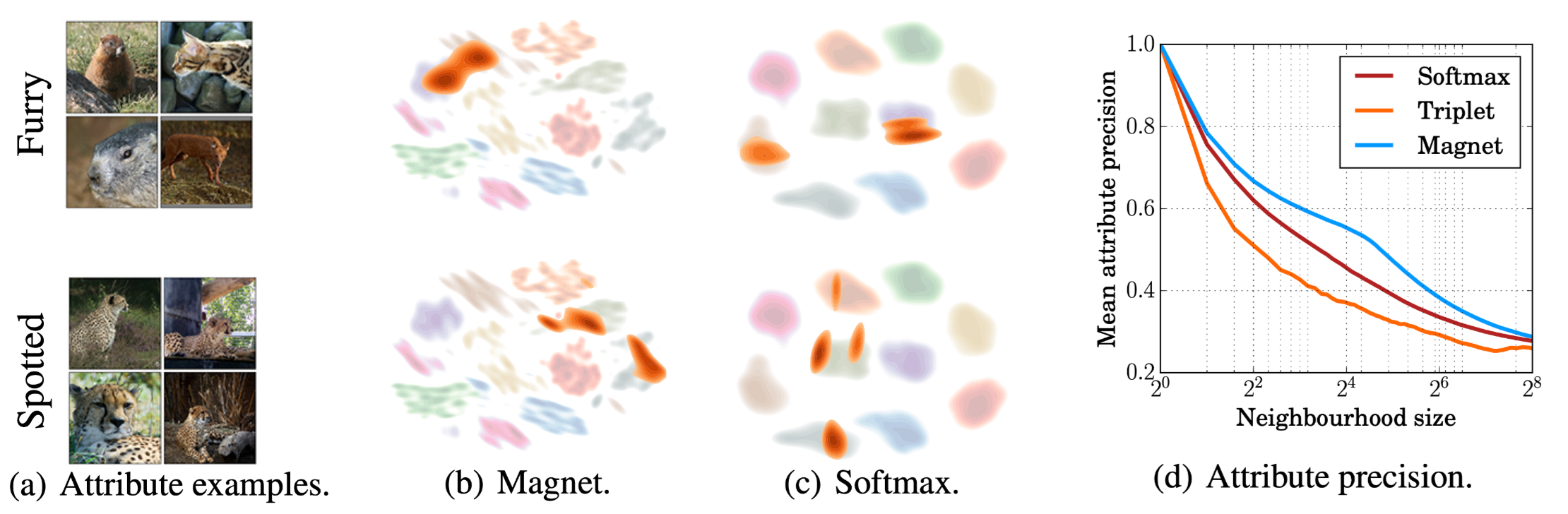
在本文中所使用的Magnet可以使不同类别中相似的样本embedding更为接近,同一类别里面不相似的样本距离更远。为了验证这一假设,作者在一个带有属性标签的数据集上进行了实验。如下图(a)所示,除了图片的正常标签外,还有一个attribute 标签,可以看到同一个attrubute标签可以包含不同类别的样本。
然后作者在训练时完全不使用attribute标签,然后通过计算一个样本的周围邻居中和它属性标签相同的所占比例来评估算法有没有学到这种类间的相似性。下图中的(c)里面显示Magnet loss可以学到这种类别间的相似性。同时,还可以注意到,Softmax的效果要好于Triplet loss。这是因为Triplet loss严格定义了样本间要么相似,要么就不相似,所以很难学到不同类样本间的相似性。而Softmax的简单设计则是为样本之间的相似性留出了空间。
下图(b)展示了Magnet 和 softmax loss学习之后的embedding,橘色表示同attribute label的样本。可以看到Magnet可以学到跨类别的相似性。
Hierarchy recovery
在这个实验中,作者想看看这个算法能不能学习到类别的层次性,能不能识别出类内的差异性。作者将两个不同类别的样本放在一起,用同一个粗化的标签替代它们原来的标签,想看一下是否能从表征中恢复原来的更精细的标签。实验结果如下。可以看到Softmax又一次好于Triplet。
